| |
Lauflängenkodierung |
| |
Eine sehr einfache Art zur Speicherung vonZeichenfolgen in einer kompakteren Formist die Lauflängenkodierung.
Folgenvon sich wiederholenden Zeichen (=Läufe, runs) werden durch die Angabedes Zeichens und die Anzahl der Wiederholungen kodiert. |
| |
Gegeben seifolgende Zeichenfolge:
aaaabbbaabbbbbccccccccdabcbaaabbbbcccd |
| |
Läufe (= Folgen von gleichen Zeichen, runs)zusammenfassen
4a3baa5b8cdabcb3a4b3cd |
| |
Binäre Dateien:
0000000000000000000011111111111100000
Länge: 37
Abwechselnd Läufe von 0 und 1 Kodierung (5-Bit):
20 12 5 = 10100 01100 00101
Länge: 15 |
| |
| Für binäre Dateien ist die Lauflängenkodierung besonders gut geeignet: man kann die Tatsache ausnützen, dass sich Läufe zwischen 0 und 1 abwechseln. Die Angabe des Zeichens (0 oder 1) kann daher entfallen. |
| |
• Binäre Dateien: 00000001111
• Binäre Dateien: 00110000010
Je mit Länge: 11 |
| |
Lösung, Kodierung (5-Bit):
• 7 4 = 00111 00100 Länge: 10
• 2 2 5 1 1 = 00010 00010 00101 00001 00001 Länge: 25
Die Lauflängenkodierung funktioniert gut, wenn die meisten Läufe lang sind, d.h. wenn die Läufe länger sind
als die Anzahl der Bits, die zur Darstellung der Binärzahl für die Anzahl der Wiederholungen notwendig sind. |
| |

Idee:
Je häufiger ein Zeichen vorkommt, desto kürzer soll sein Code sein. Anstatt nun für jedes Zeichen dieselbe Anzahl
von Bits zu benutzen, sollen Zeichen, die im Text häufiger vorkommen mit weniger Bits dargestellt werden als seltenere Zeichen.
Ein bekanntes Beispiel dafür ist der Morsecode, welcher von Prof. S.Morse (1791-1872 / USA) entdeckt wurde. |
| |
Z.B das A wird mit einem Code der Länge 2 und das E mit einem Code der
Länge 1 kodiert.
Für die Kodierung von Q und X benötigt man hingegen
einen Code der Länge 4.
Problem beim Weglassen der „Pause“
•••••–•–•• •–••––– → EEEEETETEEETEETTT
•••••–•–•• •–••––– → ISTRERAM
•••••–•–•• •–••––– → HRBXM
•••••–•–•• •–••––– → IIAAIAIO … usw. …
Geg. Zeichenfolge: MISSSWISS
Wir ermitteln die Häufigkeit der Zeichen in der Zeichenfolge: „S" und „I„ kommen am häufigsten vor, sollten daher einen möglichst kurzen Code haben.
Häufigkeiten: 5xS 2xI 1xW 1xM
S: 1 I: 0 W: 01 M: 00
Kodierung: |
 |
| |
0010111010011 Länge: 13
Lässt man die Begrenzer (Pause) weg, ist die Dekodierung aber nicht mehr eindeutig möglich:
0010011101001=IWWSSWMSS
wäre z.B. ebenso denkbar.
Kein Code ist Präfix eines anderen. Wie kann man das leicht erkennen?
Damit eine Kodierung variabler Länge eindeutig dekodierbar ist, darf kein Code ein Präfix eines anderen sein.
Beispiel: MISSSWISS (9 Symb.) |
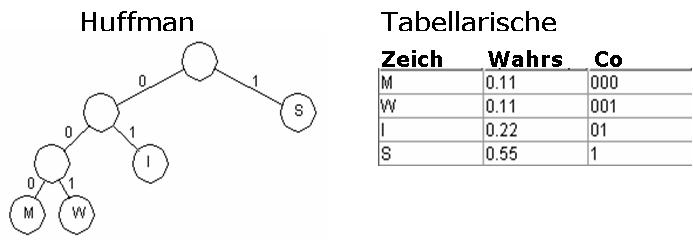 |
| |

Der Huffman-Code wird in drei einfachen Schritten aufgebaut.
1. Häufigkeit der Zeichen ermitteln
2. Aufbau des Kodierungsbaums gemäß der Häufigkeiten
3. Ableitung des Huffman-Codes
Anschließend kann der Text mit den erhaltenen Codes auf einfache Art kodiert und dekodiert werden. Die Codes müssen allerdings mitgespeichert werden.
Huffman Code wurde von Prof. David A. Huffman (1925-1999 / USA) entdeckt. |
| |

